My research centers on advancing AI-assisted mathematical proof, autoformalization, formal verification, and interpretable reasoning as interrelated approaches to aligning AI systems with human values. These directions directly address the pressing challenge of LLM opacity and the need for provably beneficial AI. While large language models (LLMs) exhibit remarkable capabilities, they largely remain “black boxes”—deep, inscrutable systems whose reasoning processes are hidden [Jiang et al., 2023b]. This opacity poses serious risks in safety-critical domains[Han et al., 2021], eroding trust and allowing subtle errors to go unnoticed. My recent research on LLM-as-judge confirms the unreliability of LLM-based evaluations widely adopted in research settings [Feuer et al., 2025]. My submission to Neurips 2025 MathAI workshop "StreetMath: Study of LLMs’ Approximation Behaviors" investigates approximation behaviors in LLMs and reveals their divergence from human reasoning patterns in everyday contexts,
Warning
Problem: The current name of your GitHub Pages repository ("Solution: Please consider renaming the repository to "
http://".
However, if the current repository name is intended, you can ignore this message by removing "{% include widgets/debug_repo_name.html %}" in index.html.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "Education
-
University of North Carolina at Chapel HillM.S. in Computer Science2009 - 2011 -
National Central UniversityB.S. in Computer Science2005 - 2009
Experience
-
SambaNova SystemsSenior Principal Software Engineer2024 - present -
Stability AIStaff Software Engineer2023 - 2024 -
TwilioStaff Software Engineer2019 - 2022 -
AmazonSoftware Engineer2017 - 2019
News
Selected Publications (view all )
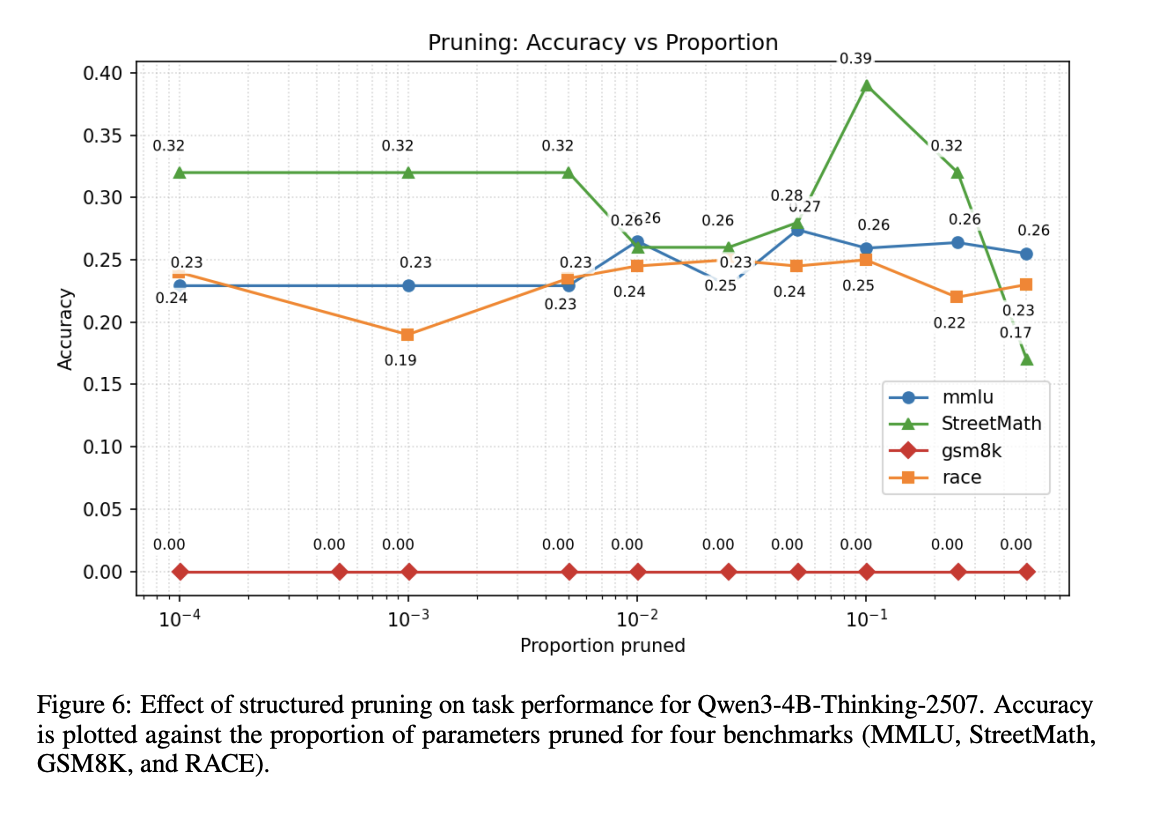
StreetMath: Study of LLMs’ Approximation Behaviors Neurips 2025 - MathAI Workshop Poster
Chiung-Yi Tseng, Somshubhra Roy, Maisha Thasin, Blessing Effiong, Danyang Zhang
There is a substantial body of literature examining the mathematical reasoning capabilities of large language models (LLMs); particularly their performance on precise arithmetic operations in autoregressive architectures. However, their ability to perform approximate reasoning in informal fast-paced mathematical operations has received far less attention, especially among non-transformer models. Our work addresses this gap by introducing StreetMath, a benchmark designed to evaluate models’ approximation abilities under real-world approximation scenarios. We conduct extensive evaluations across different LLM architectures: Qwen3-4B-Instruct-2507, Qwen3-4B-Thinking-2507, Dream-v0-Instruct-7B, Falcon-Mamba-7B-Instruct and mamba-GPT-3B. Furthermore, we apply mechanistic interpretability techniques to probe their internal computational states. Our analysis reveals that LLMs generally attempt to compute exact values or invoke external tools even in tasks that call for approximation. Moreover, while models sometimes reach the correct answer in early layers or steps, they still consume more tokens when solving approximation tasks. Additional experiments indicate that exact and approximate arithmetic operations rely on largely separate neural components. These findings suggest that LLMs’ limited performance in approximation scenarios may stem from training corpora that predominantly emphasize exact arithmetic. Drawing upon research on cognitive psychology, we argue that LLMs do not exhibit cognitive miserliness in the same way humans do in street math settings. We open source our work https://github.com/ctseng777/StreetMath
StreetMath: Study of LLMs’ Approximation Behaviors Neurips 2025 - MathAI Workshop Poster
Chiung-Yi Tseng, Somshubhra Roy, Maisha Thasin, Blessing Effiong, Danyang Zhang
There is a substantial body of literature examining the mathematical reasoning capabilities of large language models (LLMs); particularly their performance on precise arithmetic operations in autoregressive architectures. However, their ability to perform approximate reasoning in informal fast-paced mathematical operations has received far less attention, especially among non-transformer models. Our work addresses this gap by introducing StreetMath, a benchmark designed to evaluate models’ approximation abilities under real-world approximation scenarios. We conduct extensive evaluations across different LLM architectures: Qwen3-4B-Instruct-2507, Qwen3-4B-Thinking-2507, Dream-v0-Instruct-7B, Falcon-Mamba-7B-Instruct and mamba-GPT-3B. Furthermore, we apply mechanistic interpretability techniques to probe their internal computational states. Our analysis reveals that LLMs generally attempt to compute exact values or invoke external tools even in tasks that call for approximation. Moreover, while models sometimes reach the correct answer in early layers or steps, they still consume more tokens when solving approximation tasks. Additional experiments indicate that exact and approximate arithmetic operations rely on largely separate neural components. These findings suggest that LLMs’ limited performance in approximation scenarios may stem from training corpora that predominantly emphasize exact arithmetic. Drawing upon research on cognitive psychology, we argue that LLMs do not exhibit cognitive miserliness in the same way humans do in street math settings. We open source our work https://github.com/ctseng777/StreetMath
Dream Diary: Case Study on Diffusion LLM’s Arithmetic Behavior Neurips 2025 - WiML Workshop Poster
Chiung-Yi Tseng, Maisha Thasin, Blessing Effiong, Somshubhra Roy, Danyang Zhang
Mechanistic interpretability studies of autoregressive (AR) models are abundant, while studies on diffusion models (DLLM) remain less explored. In this study, we investigate the arithmetic behaviors of Dream-v0-Instruct-7B (Dream). Future work includes causal study of DLLM to isolate the arithmetic neurons [1], particularly approximation operations, extending the evaluation to larger benchmarks to gain statistical significance and providing mechanistic interpretability study tools to the community.
Dream Diary: Case Study on Diffusion LLM’s Arithmetic Behavior Neurips 2025 - WiML Workshop Poster
Chiung-Yi Tseng, Maisha Thasin, Blessing Effiong, Somshubhra Roy, Danyang Zhang
Mechanistic interpretability studies of autoregressive (AR) models are abundant, while studies on diffusion models (DLLM) remain less explored. In this study, we investigate the arithmetic behaviors of Dream-v0-Instruct-7B (Dream). Future work includes causal study of DLLM to isolate the arithmetic neurons [1], particularly approximation operations, extending the evaluation to larger benchmarks to gain statistical significance and providing mechanistic interpretability study tools to the community.
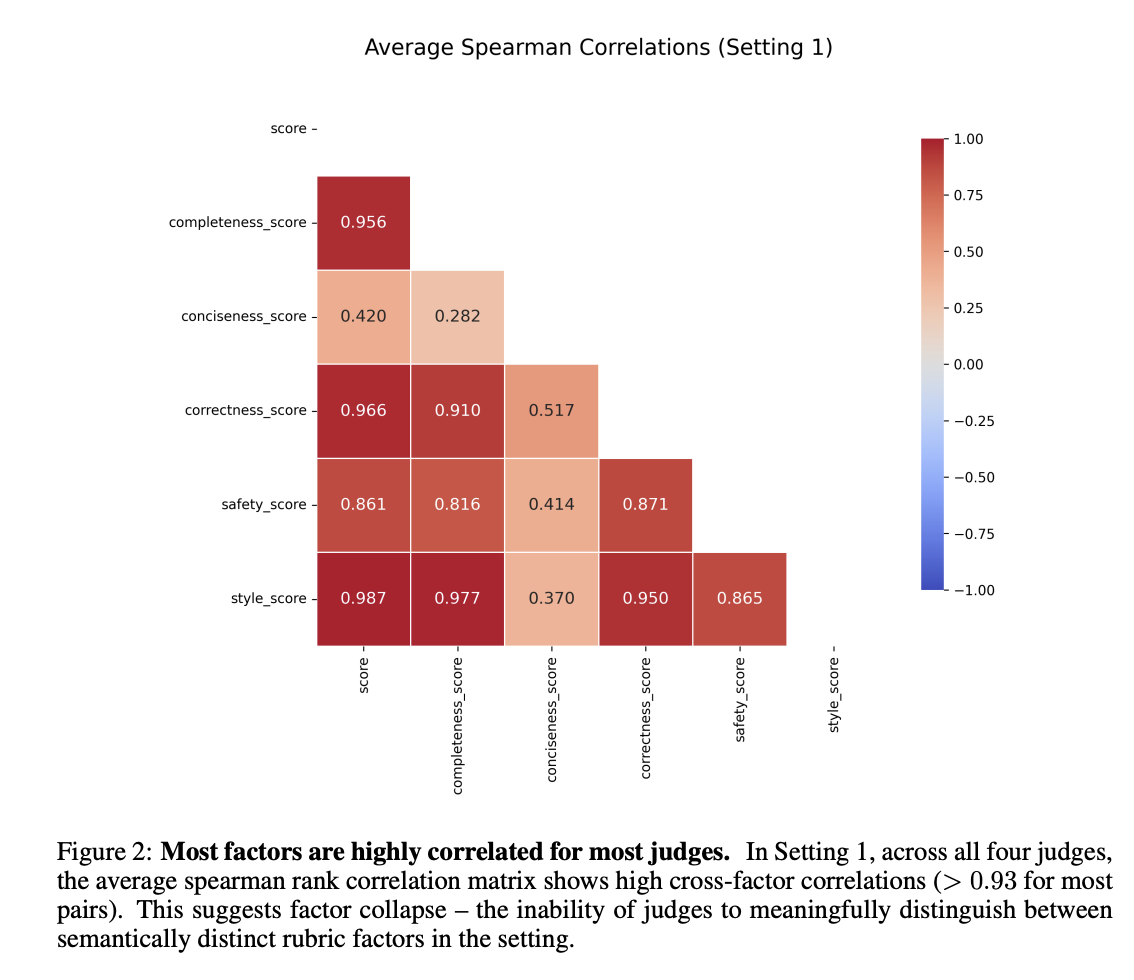
When Judgment Becomes Noise: How Design Failures in LLM Judge Benchmarks Silently Undermine Validity (Under Review) arXiv preprint Under Review
Benjamin Feuer, Chiung-Yi Tseng, Astitwa Sarthak Lathe, Oussama Elachqar, John P Dickerson
LLM-judged benchmarks are increasingly used to evaluate complex model behaviors, yet their design introduces failure modes absent in conventional, groundtruth–based benchmarks. We argue that, without tight objectives and verifiable constructions, benchmark rankings can produce high-confidence rankings that are in fact largely noise. We introduce two mechanisms to diagnose these issues. Schematic adherence quantifies how much of a judge’s overall verdict is explained by the explicit evaluation schema, revealing unexplained variance when judges deviate from their own rubric. Psychometric validity aggregates internal consistency and discriminant validity signals to quantify irreducible uncertainty in any benchmarking run. Applying these tools to Arena-Hard Auto, we find severe schema incoherence and factor collapse across popular judges: e.g., unexplained variance exceeding 90% for DeepSeek-R1-32B and factor correlations above 0.93 for most criteria. We also show that the ELO-style aggregation used by Arena-Hard Auto collapses and masks genuine ranking uncertainty. Our results highlight design failures that undermine validity and offer actionable principles for building better-scoped, reliability-aware LLM-judged benchmarks. We release our code at https://anonymous.4open.science/r/judgment-to-noise-947D/README.md
When Judgment Becomes Noise: How Design Failures in LLM Judge Benchmarks Silently Undermine Validity (Under Review) arXiv preprint Under Review
Benjamin Feuer, Chiung-Yi Tseng, Astitwa Sarthak Lathe, Oussama Elachqar, John P Dickerson
LLM-judged benchmarks are increasingly used to evaluate complex model behaviors, yet their design introduces failure modes absent in conventional, groundtruth–based benchmarks. We argue that, without tight objectives and verifiable constructions, benchmark rankings can produce high-confidence rankings that are in fact largely noise. We introduce two mechanisms to diagnose these issues. Schematic adherence quantifies how much of a judge’s overall verdict is explained by the explicit evaluation schema, revealing unexplained variance when judges deviate from their own rubric. Psychometric validity aggregates internal consistency and discriminant validity signals to quantify irreducible uncertainty in any benchmarking run. Applying these tools to Arena-Hard Auto, we find severe schema incoherence and factor collapse across popular judges: e.g., unexplained variance exceeding 90% for DeepSeek-R1-32B and factor correlations above 0.93 for most criteria. We also show that the ELO-style aggregation used by Arena-Hard Auto collapses and masks genuine ranking uncertainty. Our results highlight design failures that undermine validity and offer actionable principles for building better-scoped, reliability-aware LLM-judged benchmarks. We release our code at https://anonymous.4open.science/r/judgment-to-noise-947D/README.md
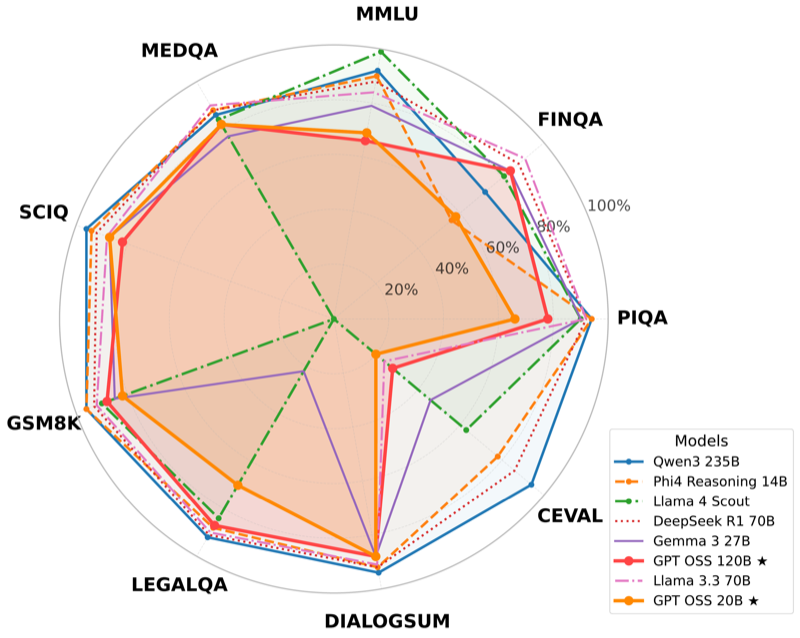
Is GPT-OSS Good? A Comprehensive Evaluation of OpenAI's Latest Open Source Models arXiv preprint
Ziqian Bi*, Keyu Chen*, Chiung-Yi Tseng*, Danyang Zhang*, Tianyang Wang, Hongying Luo, Lu Chen, Junming Huang, Jibin Guan, Junfeng Hao, Junhao Song (* equal contribution)
This paper evaluates OpenAI's first open weight large language models since GPT-2, comparing two mixture of experts models (120B and 20B parameters) against six contemporary open source models. Our comprehensive evaluation reveals that gpt-oss-20B consistently outperforms gpt-oss-120B on several benchmarks, providing important insights into the performance characteristics of these newly released models.
Is GPT-OSS Good? A Comprehensive Evaluation of OpenAI's Latest Open Source Models arXiv preprint
Ziqian Bi*, Keyu Chen*, Chiung-Yi Tseng*, Danyang Zhang*, Tianyang Wang, Hongying Luo, Lu Chen, Junming Huang, Jibin Guan, Junfeng Hao, Junhao Song (* equal contribution)
This paper evaluates OpenAI's first open weight large language models since GPT-2, comparing two mixture of experts models (120B and 20B parameters) against six contemporary open source models. Our comprehensive evaluation reveals that gpt-oss-20B consistently outperforms gpt-oss-120B on several benchmarks, providing important insights into the performance characteristics of these newly released models.